Problem Restatement
This part mainly introduces the principle and realization method of GAN (Generative Adversarial Nets), GAN is proposed by lan.J et al. In 2014, they propose a new framework for estimating generative models via an adversarial process, in which simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that a sample came from the training data rather than G. The training procedure for G is to maximize the probability of D making a mistake. This framework corresponds to a minimax two-player game. In the space of arbitrary functions G and D, a unique solution exists, with G recovering the training data distribution and D equal to 1/2 everywhere. In the case where G and D are defined by multilayer perceptron’s, the entire system can be trained with backpropagation. There is no need for any Markov chains or unrolled approximate inference net-works during either training or generation of samples[1].
It can be said that the past few years in the field of machine learning the brightest and hottest new idea is to generate a confrontation network. This idea not only gave birth to a lot of theoretical papers, but also brought an endless practical application. Yann LeCun himself has been generously praised: This is the best idea of the past few years! So we chose GAN as one of our research contents.
Method Introduction
First of all, introduce the generative model, which in the history of machine learning has been occupying a pivotal position. When we have a lot of data, such as images, voice, text, etc., if the model can help us to simulate the distribution of these high-dimensional data, then for many applications will be of great benefit.
For scenarios where the amount of data is scarce, generating models can help generate data and increase the number of data, thereby improving learning efficiency using semi-supervised learning. Language model is one of the widely used examples of generation model. Through reasonable modeling, language model can not only help to generate language fluent sentences, but also has a wide range of auxiliary applications in machine translation, chat dialogue and other research fields.
GAN uses the maximum likelihood estimate to create the model:
$$\theta^*=\mathop{argmax}\limits_{\theta}E_{x \sim p_{data}}log_{p_{model}}(x|\theta)$$
We all know that the probability of simultaneous occurrence of a group of independent events is:
$$P(X_1,X_2)=P(X_1) \times P(X_2)$$
And in real life, we probably do not know what each P (probability distribution model) is, we know that we can observe the source data. So, the maximum likelihood estimate is the way that gives the observation data to evaluate the model parameters (that is, how the distribution model should be estimated). First, suppose we independently sample $X_1,X_2,⋯X_n$ and we use the f model, but its argument θ is unknown, then this equation can be expressed as:
$$f(X_1,X_2,…X_n|\theta)=\prod f(X_i|\theta)$$
Take the logarithm on both sides:
$$\log L(\theta|X_1,X_2,…X_n)=\sum logf(X_i|\theta)$$
Set:
$$\overline{\varphi}=\frac{1}{n}\log L$$
$\log L(\theta|X_1,X_2,…X_n)$ called logarithmic likelihood, $\overline{\varphi}$ called average log likelihood. Then the largest average logarithmic likelihood is:
$$\overline{\theta}_{mL}=argmax\hat{\varphi}(\theta | X_1,X_2,…X_n)$$
That is the meaning of the first formula.
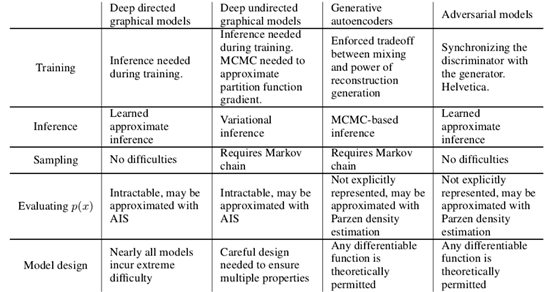
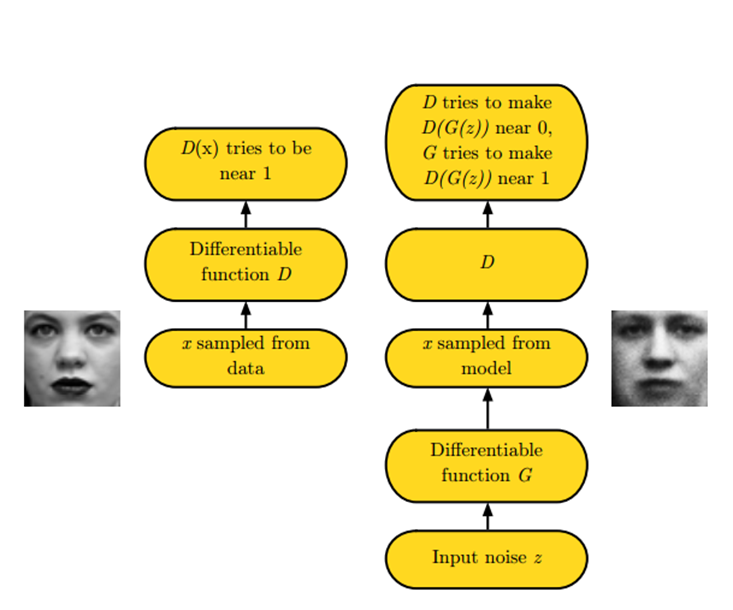
Most powerful generation models require the use of the Markov chain, and GAN is the only one-to-one generation model that is directly observed from data. To understand the generation of the confrontation model (GAN), we must first know that the generation of the confrontation model is two things: one is the discriminant model and one is the model.
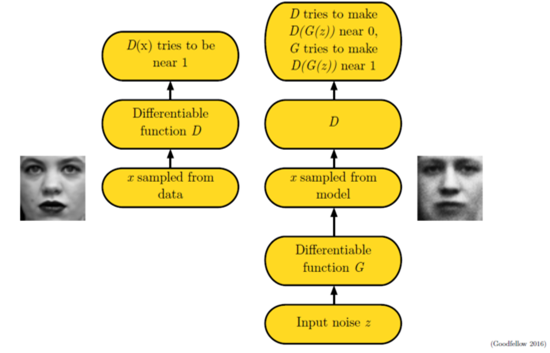
For example, we have some real data, but also a mess of false data. A effort to take the fake data from hand to imitate the real data, and rub into the real data. B is desperately trying to distinguish between real and false data. Here, A is a generation model, the goal is to fool the recognition of B. And B is a discriminant model, trying to distinguish all the false data. So, with the B’s identification skills more and more powerful, A forged data skills are more and more skilled. Where A is the generative model:
$$x=G(z;\theta^{(G)})$$
Here is our generation model. As shown, it disguises the real data x by generating the model G by generating the noise data z (that is, the false data we say). Of course, because GAN is still a neural network, the generation model needs to be differentiable.
The process of training is also very intuitive, we can use SGD-like algorithm of choice on two minibatches simultaneously: A minibatch of training examples and A minibatch of generated samples. Of course, we can also train a set of each run, the other group is running K times, this can prevent one of them cannot keep up with the rhythm.
Similarly, since the use of SGD optimization, we need an objective function to determine and monitor the results of learning. Here, $J(D)$ represents the objective function of the discriminant network a cross entropy function. Where the left part indicates that D judges that x is true x and the right part indicates the case where the noise data z is forged by the generated network G identified by D.
$$J^{(D)}=-\frac{1}{2}E_{x \sim p_{data}}\log D(x)-\frac{1}{2}E_z\log (1-D(G(z)))$$
In this way, the same, $J(G)$ is the representative of the network to generate the objective function, its purpose is to follow the anti-D, so in front of a negative sign[2]:
$$J^{(G)}=-J^{(D)}$$
A more intuitive explanation of this process is as follows: suppose that at the beginning of the training, the true sample distribution, the generated sample distribution, and the discriminant model are black lines, green lines, and blue lines in the figure, respectively. It can be seen that at the beginning of the training, the discriminant model is not well distinguishable from the real sample and the resulting sample. Then when we build the model fixedly, and the optimization of the model, the optimization results as shown in the second picture, we can see that this time the discriminant model has been able to better distinguish between the generation of data and real data. The third step is to fix the discriminant model, improve the generation model, and try to let the discriminant model cannot distinguish between the generated picture and the real picture. In this process, we can see that the image distribution generated by the model is closer to the real picture distribution. , Until the final convergence, generated distribution and true distribution coincidence[3].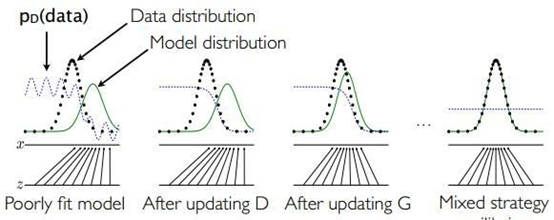
Environment of Reproduction
Environment
- Windows 10.1 Professional
- i7-6700HQ CPU @ 2.60GHz x8
- Src in
Python 3.5.xwithJupyter notebook
Requirement
- tensorflow (1.1.0)
- numpy (1.11.3)
- matplotlib (2.0.0)
- seaborn (0.7.1)
- scipy (0.18.1)
Result of Reproduction
We trained adversarial nets an a range of datasets including MNIST[4], the Toronto Face Database (TFD)[5], and CIFAR-10 [6]. The generator nets used a mixture of rectifier linear activations[7][8] and sigmoid activations, while the discriminator net used maxout[9] activations. Dropout [10] was applied in training the discriminator net. While our theoretical framework permits the use of dropout and other noise at intermediate layers of the generator, we used noise as the input to only the bottommost layer of the generator network.
We estimate probability of the test set data under pgby fitting a Gaussian Parzen window to the samples generated with G and reporting the log-likelihood under this distribution. The σ parameter of the Gaussians was obtained by cross validation on the validation set. This procedure was introduced in Breuleux et al. [11] and used for various generative models for which the exact likelihood is not tractable[12][13][14]. Results are reported in Table 1. This method of estimating the likelihood has somewhat high variance and does not perform well in high dimensional spaces but it is the best method available to our knowledge. Advances in generative models that can sample but not estimate likelihood directly motivate further research into how to evaluate such models.
Table 1 Parzen window-based log-likelihood estimates. The reported numbers on MNIST are the mean log-likelihood of samples on test set, with the standard error of the mean computed across examples. On TFD, we computed the standard error across folds of the dataset, with a different σ chosen using the validation set of each fold. On TFD, σ was cross validated on each fold and mean log-likelihood on each fold were computed. For MNIST we compare against other models of the real-valued (rather than binary) version of dataset.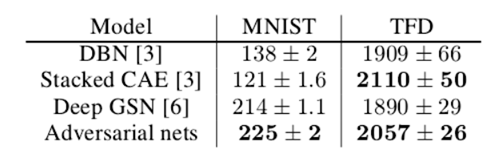
In Figures 1 and 2 we show samples drawn from the generator net after training. While we make no claim that these samples are better than samples generated by existing methods, we believe that these samples are at least competitive with the better generative models in the literature and highlight the potential of the adversarial framework.
Rightmost column shows the nearest training example of the neighboring sample, in order to demonstrate that the model has not memorized the training set. Samples are fair random draws, not cherry-picked. Unlike most other visualizations of deep generative models, these images show actual samples from the model distributions, not conditional means given samples of hidden units. Moreover, these samples are uncorrelated because the sampling process does not depend on Markov chain mixing.

Besides the Reproduction above from authors of the essay, we also try to achieve a toy model of GAN on Gaussian Distribution.
###Figures of Testing Model
Initial
Initially, generate $P_{data}$ and original decision boundary: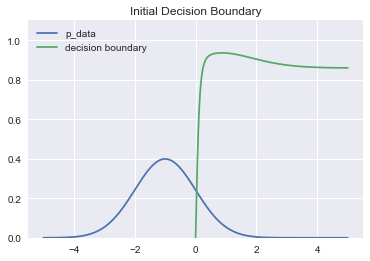
Pre-train Decision Surface
If decider is reasonably accurate to start, we get much faster convergence.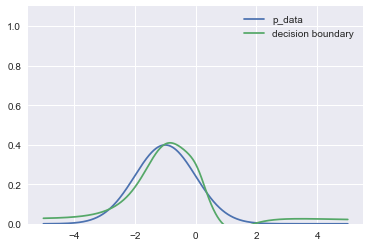
Training Loss
Loss Value during iteration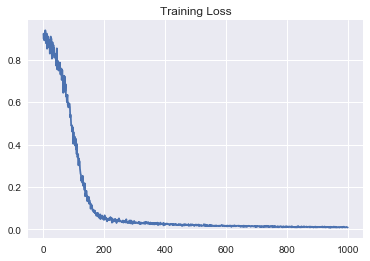
Iteration
After 10,000 iters (Inspite of faster presentation, during less than 15 secs. in this method):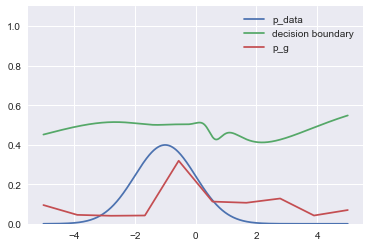
The Outlook for the essay
Reference
[1] Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in neural information processing systems. 2014: 2672-2680.
[2] http://www.sohu.com/a/121189842_465975
[3] https://baijiahao.baidu.com/po/feed/share?wfr=spider&for=pc&context=%7B%22sourceFrom%22%3A%22bjh%22%2C%22nid%22%3A%22news_3737750434789358240%22%7D
[4] LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
[5] Susskind, J., Anderson, A., and Hinton, G. E. (2010). The Toronto face dataset. Technical Report UTML TR 2010-001, U. Toronto.
[6] Krizhevsky, A. and Hinton, G. (2009). Learning multiple layers of features from tiny images. Technical report, University of Toronto.
[7] Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). What is the best multi-stage architecture for object recognition? In Proc. International Conference on Computer Vision (ICCV’09), pages 2146–2153.IEEE.
[8] Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse rectifier neural networks. In AISTATS’2011.
[9] Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. (2013a). Maxout networks.In ICML’2013.
[10] Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2012b). Improving neural networks by preventing co-adaptation of feature detectors. Technical report, arXiv:1207.0580.
[11] Breuleux, O., Bengio, Y., and Vincent, P. (2011). Quickly generating representative samples from an RBM-derived process. Neural Computation, 23(8), 2053–2073.
[12] Rifai, S., Bengio, Y., Dauphin, Y., and Vincent, P. (2012). A generative process for sampling contractive auto-encoders. In ICML’12.
[13] Bengio, Y., Mesnil, G., Dauphin, Y., and Rifai, S. (2013a). Better mixing via deep representations. In ICML’13.
[14] Bengio, Y., Thibodeau-Laufer, E., and Yosinski, J. (2014a). Deep generative stochastic networks trainable by backprop. In ICML’14.
GAN的结构
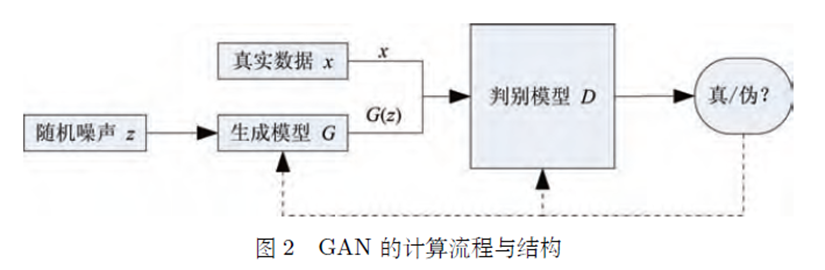
要理解生成对抗模型(GAN),首先要知道生成对抗模型拆开来是两个东西:一个是判别模型,一个是生成模型。
左面是我们的判别模型,右面是生成模型
判别模型即输入一个样本,判断它与真实的模型相似度是多少,越相似越接近于1
而生产模型则是输入一个噪音,通过过生成器来生成一个样本,然后让判别模型判别。那么训练就是让判别函数判别该样本是生成的,而生成器则尽力让它生成的样本接近于真实样本,也就是让图中的 $D(G(z))$ 接近于1
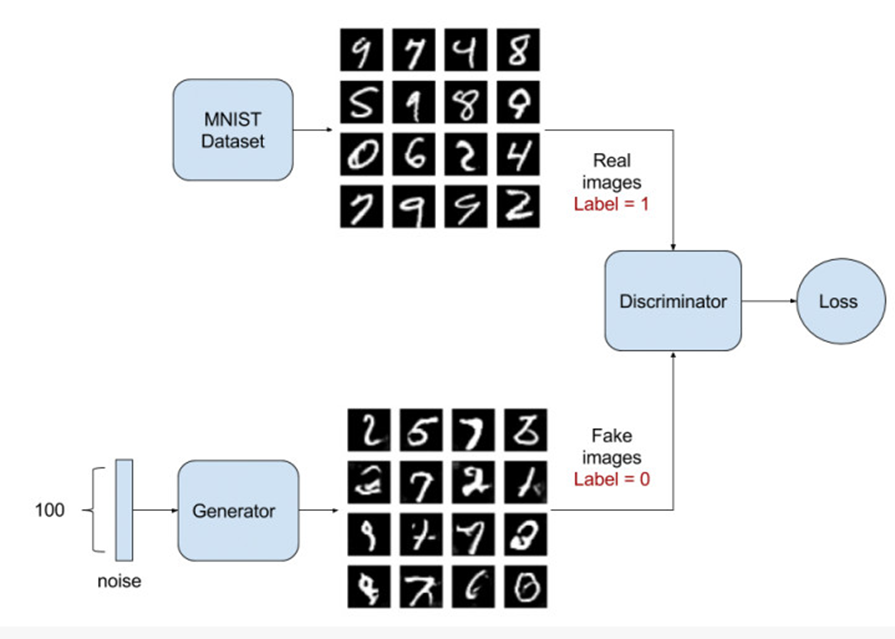
以NMIST为例
判别器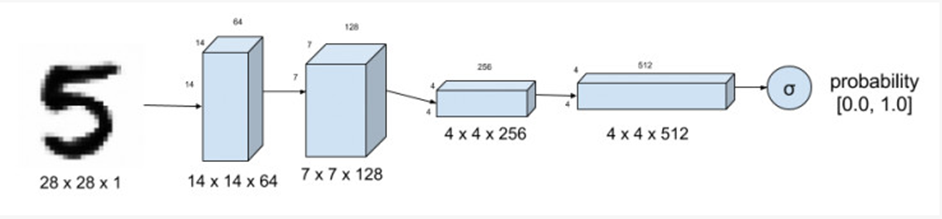
生成器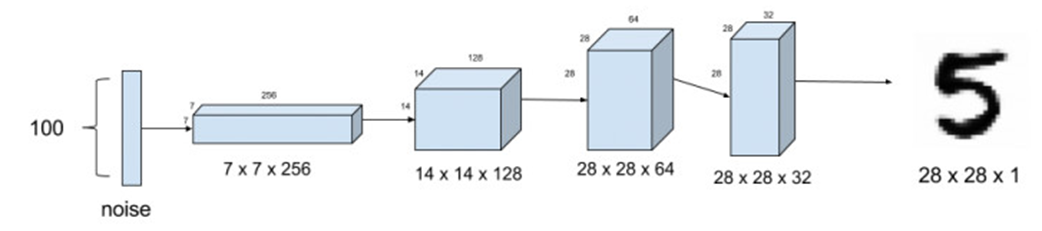
GAN的训练

$$\triangledown_{\theta_{d}}\frac{1}{m}\sum_{i=1}^{m}\left[\log D(x^{(i)})+\log(1-D(G(z^{(i)})))\right]$$
其中对抗模型的训练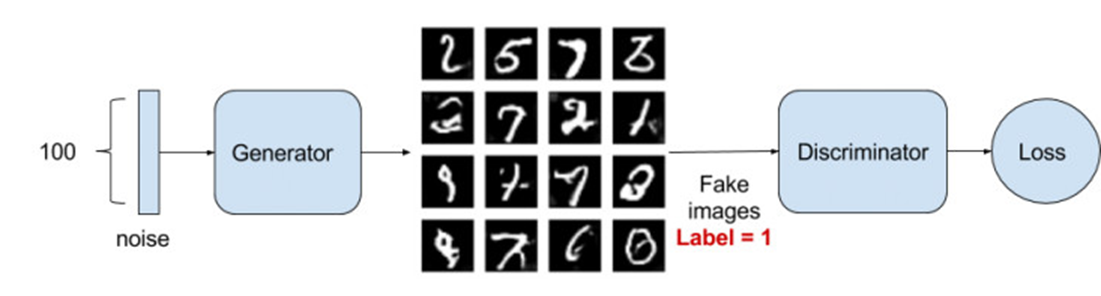
$$\triangledown_{\theta_{g}}\frac{1}{m}\sum_{i=1}^{m}\log(1-D(G(z^{(i)})))$$
训练的过程也非常直观,你可以选择任何类 SGD 的方法(因为 A 和 B 两个竞争者都是可微的网络)。并且你要同时训练两组数据:一组真实的训练数据和一组由骗子 A 生成的数据。
同样,既然要用类 SGD 优化,我们就需要一个目标函数(objective function)来判断和监视学习的成果。在这里,$J(D)$ 代表判别网络(也就是警察 B)的目标函数——一个交叉熵(cross entropy)函数。其中左边部分表示 D 判断出 x 是真 x 的情况,右边部分则表示 D 判别出的由生成网络 G(也就是骗子)把噪音数据 z 给伪造出来的情况。
这样,同理,$J(G)$ 就是代表生成网络的目标函数,它的目的是跟 D 反着干,所以前面加了个负号(类似于一个 Jensen-Shannon(JS)距离的表达式)。
我们定义输入噪声的先验变量$p_z(z)$,然后使用$G(z;θ_g)$来代表数据空间的映射。这里G是一个由含有参数$\theta_g$的多层感知机表示的可微函数。我们再定义了一个多层感知机$D(x;θ_d)$用来输出一个单独的标量。D(x) 代表x 来自于真实数据分布而不是$p_g$的概率,我们训练D来最大化分配正确标签给不管是来自于训练样例还是G生成的样例的概率.我们同时训练G来最小化$log(1−D(G(z)))$。换句话说,D和G的训练是关于值函数V(G,D)的极小化极大的二人博弈问题
Discriminator Strategy
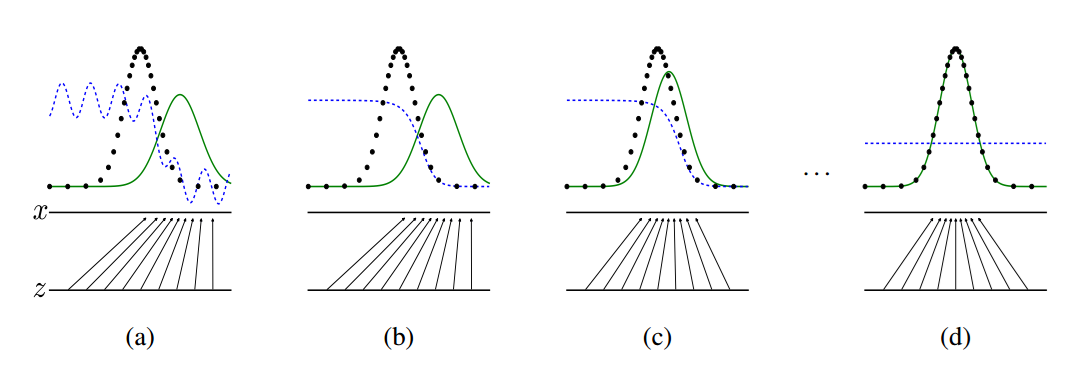

如图所示,我们手上有真实数据(黑色点,data)和模型生成的伪数据(绿色线,model distribution,是由我们的 z 映射过去的)(画成波峰的形式是因为它们都代表着各自的分布,其中纵轴是分布,横轴是我们的 x)。而我们要学习的 D 就是那条蓝色的点线,这条线的目的是把融在一起的 data 和 model 分布给区分开。写成公式就是 data 和 model 分布相加做分母,分子则是真实的 data 分布。
我们最终要达到的效果是:D 无限接近于常数 1/2。换句话说就是要 Pmodel 和 Pdata 无限相似。这个时候,我们的 D 分布再也没法分辨出真伪数据的区别了。这时候,我们就可以说我们训练出了一个炉火纯青的造假者(生成模型)。
The Optimal Discriminator
For G fixed, the optimal discriminator D is:
$$ D_G^*(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)} $$
Differentiate:
$$ -P_r(x)\log D(x)-P_g(x)\log [1-D(x)] $$